Vector Multiplied by Matrix Again and Again Theorem

Age 16 to 18

Published 2004 Revised 2008

Vectors - What Are They? gives an introduction to the subject.

There are two useful definitions of multiplication of vectors, in one the product is a scalar and in the other the product is a vector. There is no operation of division of vectors. In some school syllabuses you volition come across scalar products but not vector products but we discuss both types of multiplication of vectors in this commodity to give a more rounded picture of the basics of the subject area

Scalar Multiplication

The scalar production of vectors ${\bf u} = (u_1, u_2, u_3)$ and ${\bf v}=(v_1, v_2, v_3)$ is a scalar defined to be $${\bf u.five}= u_1v_1 + u_2v_2 + u_3v_3\quad (1).$$ This is sometimes called the inner product or dot product . It follows immediately from the definition that $${\bf u.u} = u_1^2+u_2^2+u_3^2=|{\bf u}|^2 \quad (2),$$ and if ${\bf i, j, k}$ are unit vectors along the axes then $${\bf i.i}={\bf j.j} = {\bf k.k} = ane,\quad {\rm and}\quad {\bf i.j}={\bf j.k} = {\bf k.i} = 0\quad (3).$$ It is left to the reader to check from the definition that $${\bf u.5} = {\bf 5.u}, \ {\rm and} \ ({\bf u + 5}).{\bf westward} = {\bf u.w}+{\bf v.w}.$$ This shows that we can expand or multiply out $${\bf u.five}= (u_1{\bf i}+u_2{\bf j}+u_3{\bf thousand}).(v_1{\bf i}+v_2{\bf j}+u_3{\bf k})$$ giving nine terms. Using equation (3) vi of these terms are zero and the other three give the expression $u_1v_1+u_2v_2+u_3v_3$ consistent with the definition in equation (1).

The Cosine Rule in Euclidean Geometry tin exist proved without the use of scalar products. Using the Cosine Rule for the triangle $\Delta OPQ$ where $\angle POQ = \theta$ we go: $$|{\bf u-v}|^2 =|{\bf u}|^2 + |{\bf v}|^2 - ii|{\bf u}||{\bf v}|\cos \theta.\quad (4) $$

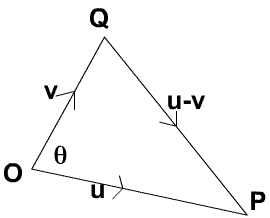
Expanding $|{\bf u-5}|^2$ nosotros become $$|{\bf u-v}|^2 = ({\bf u}-{\bf five}).({\bf u}-{\bf v})= |{\bf u}|^2 + |{\bf v}|^two - ii{\bf u}.{\bf v},\quad (five).$$ Hence, from equations (4) and (v), we get the very useful consequence $${\bf u.v} = |{\bf u}||{\bf v}|\cos \theta, \quad (6)$$ where angle $\theta$ is the angle betwixt the vectors ${\bf u}$ and ${\bf five}$. This is a very important and useful issue because it enables us to notice the angle betwixt ii vectors.

Some texts use the formula (half-dozen) to ascertain the bending between ii vectors, that is $$\theta = \cos^{-1} \left({{\bf u.v}\over |{\bf u}|||{\bf v}|}\correct)\quad (7).$$ In three dimensions nosotros can utilise a more intuitive definition of bending in terms of turning, just in higher dimensions information technology is necessary to have a definition of angle such every bit formula (vii). If we use this formula to define an angle then the Cosine Rule follows straight as the two are equivalent.

Annotation that the product of a row vector and a column vector is defined in terms of the scalar production and this is consequent with matrix multiplication. $$(u_1\ u_2\ u_3)\left( \begin{array}{cc} v_1 \\ v_2 \\ v_3 \end{array} \right) = u_1v_1 + u_2v_2 + u_3v_3.$$

Vector Multiplication

The vector production of two vectors ${\bf b}$ and ${\bf c}$, written ${\bf b}\times {\bf c}$ (and sometimes called the cross product ), is the vector $${\bf b}\times {\bf c} = \left( \begin{array}{cc} b_2c_3-b_3c_2 \\ b_3c_1 -b_1c_3 \\ b_1c_2 -b_2c_1 \end{array} \correct) \quad (8).$$ There is an alternative definition of the vector product, namely that ${\bf b}\times {\bf c}$ is a vector of magnitude $|{\bf b}||{\bf c}|\sin \theta$ perpendicular to ${\bf b}$ and ${\bf c}$ and obeying the 'right mitt rule', and we shall show that this outcome follows from the given definition and that the ii definitions are equivalent. The proof is given after for abyss but kickoff nosotros consider ${\bf b}\times {\bf c}$ expressed in terms of components in the directions of ${\bf i, j, grand}$.

From this definition we can see that ${\bf b}\times {\bf c}=-{\bf c}\times {\bf b}$ and then this operation is not commutative. If ${\bf i, j, k}$ are unit vectors along the axes so, from this definition: $${\bf i}\times {\bf i} = {\bf j}\times {\bf j}= {\bf k}\times {\bf k},$$ and $$\eqalign{ {\bf i}\times {\bf j} &= {\bf k},\quad {\bf j}\times {\bf i} = -{\bf 1000} \cr {\bf j}\times {\bf k} &= {\bf i},\quad {\bf thou}\times {\bf j} = -{\bf i} \cr{\bf thou}\times {\bf i} &= {\bf j},\quad {\bf i}\times {\bf k} = -{\bf j} .}$$ From the definition it follows that $$k({\bf b}\times {\bf c}) = (k{\bf b})\times {\bf c} = {\bf b} \times (1000{\bf c}), \quad\quad ({\bf a+b})\times {\bf c} = ({\bf a}\times {\bf c}) + ({\bf b}\times {\bf c}).$$ Expanding the expression $${\bf b}\times {\bf c} = (b_1{\bf i} + b_2{\bf j} + b_3 {\bf k}) \times (c_1{\bf i}+ c_2{\bf j} + c_3 {\bf thou})$$ gives $$ (b_2c_3-b_3c_2){\bf i}+ (b_3c_1-b_1c_3){\bf j} + (b_1c_2-b_2c_1){\bf k} \quad (9)$$ which is the formula for the vector product given in equation (8).

Now we prove that the two definitions of vector multiplication are equivalent. The diagram shows the directions of the vectors ${\bf b}$, ${\bf c}$ and ${\bf b}\times {\bf c}$ which class a 'right handed gear up'.

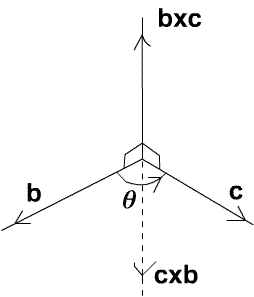
You may wish to finish reading here and information technology is indeed more important to appreciate that in that location are two definitions of a vector product, which can be shown to be equivalent, than it is mechanically to work through the details of the proof.

Theorem The vector production of 2 vectors ${\bf b}$ and ${\bf c}$ is a vector ${\bf b}\times {\bf c}$ with the following properties:

(i) ${\bf b}\times {\bf c}$ has magnitude $|{\bf b}||{\bf c}|\sin \theta$ where $\theta$ is the angle betwixt the directions of ${\bf b}$ and ${\bf c}$;

(ii) ${\bf b}\times {\bf c}$ is perpendicular to ${\bf b}$ and ${\bf c}$ with direction such that the vectors ${\bf b}$, ${\bf c}$ and ${\bf b}\times {\bf c}$ form a right handed prepare as in the diagram and then that ${\bf b}\times {\bf c}$ and ${\bf c}\times {\bf b}$ are in opposite directions.

Proof of part (i) Consider the area of the parallelogram with sides given by the vectors ${\bf b}$ and ${\bf c}$ and angle $\theta$ between these sides. The area of this parallelogram is $|{\bf b}||{\bf c}|\sin \theta$. The vector ${\bf b}$ tin be decomposed into a vector $grand{\bf c}$ of magnitude $|{\bf b}|\cos \theta$ in the direction of ${\bf c}$ and ${\bf b}-k{\bf c}$ of magnitude $|{\bf b}|\sin \theta$ perpendicular to ${\bf c}$ where $k=|{\bf b}|\cos \theta/|{\bf c}|=({\bf b.c})/|{\bf c}|^2$.

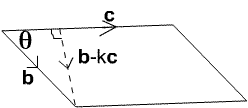
So the area of the parallelogram is: $$\eqalign{ |{\bf c}||{\bf b}|\sin \theta &= |{\bf c}||{\bf b}-k{\bf c}| \cr &= ||{\bf c}|{\bf b} - ({\bf b.c}){\bf c}/|{\bf c}||}$$ In order to work out the modulus on the correct hand side we have the scalar production of the vector with itself. $$\eqalign{ |{\bf c}||{\bf b}|\sin \theta &= (|{\bf c}|{\bf b} - ({\bf b.c}){\bf c}/|{\bf c}|).(|{\bf c}|{\bf b} - ({\bf b.c}){\bf c}/|{\bf c}|) \cr &= ({\bf b.b})|{\bf c}|^two - two({\bf b.c})^2 + ({\bf b.c})^2{\bf c.c}/|{\bf c}|^two \cr &=\sqrt{|{\bf b}|^ii|{\bf c}|^2 - ({\bf b.c})^2}\cr &=\sqrt{b_1^2+b_2^ii+b_3^2 (c_1^ii+c_2^2+c_3^2)-(b_1c_1+b_2c_2+b_3c_3)^2} \cr &=\sqrt{(b_2c_3-b_3c_2)^two+(b_3c_1-b_1c_3)^2+(b_1c_2-b_2c_1)^2} \cr &= |{\bf b}\times {\bf c}|. }$$

Proof of role (ii) To show that ${\bf b}$ and ${\bf b}\times {\bf c}$ are perpendicular we show that the scalar product is zero: $${\bf b}.{\bf b}\times {\bf c} = b_1(b_2c_3-b_3c_2) +b_2(b_3c_1-b_1c_3)+b_3(b_1c_2-b_2c_1) = 0,$$ and similarly the scalar product of ${\bf c}$ and ${\bf b}\times {\bf c}$ is zero so these vectors are perpendicular.

tisdalewaake1976.blogspot.com

Source: https://nrich.maths.org/2393

Share this post